本文翻译自论文 An Overview of Query Optimization in Relational Systems,论文介绍了 70 年代以来优化器方面的研究成果,通过本文的学习,我们可以快速了解关系系统中常见的查询优化技术,为后续深入学习 Calcite 及查询优化技术打下良好的基础。
目标
自上世纪 70 年代初以来,学术界在查询优化领域进行了大量的研究工作。在一篇简短的论文中,很难展现出这些研究工作的广度和深度。因此,我决定将重点放在关系型数据库系统的 SQL 查询优化上,并提出我对这个领域的个人看法。本文的目标不是全面的,而是介绍这个领域的基础理论,并展示这些重要工作的一些示例。我想向这个领域的贡献者们道歉,由于个人疏忽及篇幅原因,我未能明确地感谢他们的工作。此外,为了便于演示,我冒昧地牺牲了技术精度。
简介
关系查询语言提供了高级的 声明式 接口,用来访问存储在关系型数据库中的数据。随着时间的推移,SQL[1] 已经成为关系查询语言的标准。SQL 数据库系统查询计算组件的两个最关键组件是 查询优化器 和 查询执行引擎。
查询执行引擎实现了一组物理算子(physical operators)。算子负责将一个或多个数据流作为输入,并生成一个输出数据流。物理算子的例子包括:(外部)排序、顺序扫描、索引扫描、嵌套循环连接(nested-loop join) 和 排序合并连接(sort-merge join)。我将这些算子称为物理算子,因为它们不一定与关系操作符一一对应。理解物理算子最简单的方法是将它看做代码块,代码块作为基础模块实现了 SQL 查询语句的执行。这种执行的抽象表示就是物理算子树,如图 1 所示。算子树中的边表示物理算子之间的数据流。我们使用 物理算子树、执行计划(或者 简单的计划)这些可交换的术语。执行引擎负责计划的执行,并且生成查询的结果。因此,查询执行引擎的功能决定了可行的算子树的结构。读者可以参考[2]来了解查询估算技术的概要。
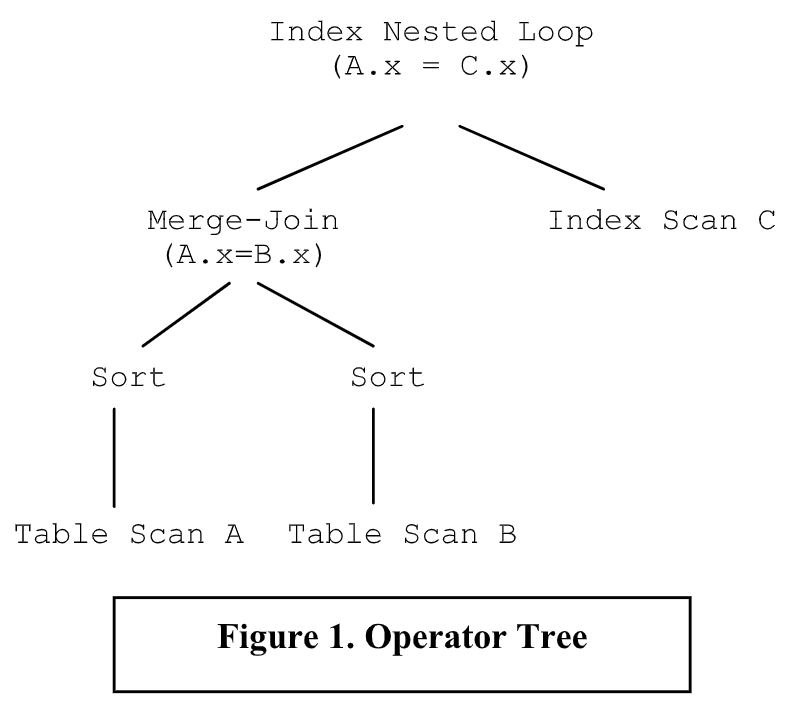
查询优化器负责为执行引擎生成输入。它接受一个已解析的 SQL 查询作为输入,并负责从可行的执行计划空间里,为给定的 SQL 查询生成有效的执行计划。优化器的任务并不简单,因为对于给定的 SQL 查询,可能存在大量可行的算子树:
- 给定查询的代数表示,可以转换为许多其他逻辑上等价的代数表示,例如:
1 | Join(Join(A,B),C) = Join(Join(B,C),A) |
- 对于一个给定的代数表示,可能有许多实现代数表达式的算子树,例如:数据库系统通常支持多种连接算法。
此外,执行这些计划的吞吐量或响应时间可能大不相同,因此,优化器对执行计划的明智选择是极其重要的。我们可以将查询优化看作是一个困难的搜索问题。为了解决这个问题,我们需要提供:
- 执行计划空间(搜索空间);
- 成本估算技术,以便为每个搜索空间中的执行计划分配成本(
cost)。直观地说,这是对执行计划所需资源的估算; - 枚举算法,用来搜索整个执行计划空间。
一个理想的优化器通常是这样的:(1)搜索空间包含低成本的执行计划;(2)成本计算技术是准确的;(3)枚举算法是有效的。这三个任务中的每一个都不是轻而易举的,这就是为什么构建一个好的优化器是一个巨大的任务。
我们首先讨论 System-R 优化框架,因为这是一种非常优雅的优化方法,有助于推动后续的优化工作。在第 4 节中,我们将讨论优化器所要考虑的搜索空间。这节将会提供一个版块,用来介绍搜索空间中包含的重要代数变换。在第 5 节中,我们将讨论成本估算的问题。在第 6 节中,我们将讨论枚举搜索空间的主题。这些小节就完成了对基本优化框架的讨论。在第 7 节中,我们将讨论查询优化方面的一些最新进展。
SYSTEM-R 优化器
SYSTEM-R 项目显著提升了关系系统查询优化的状态。[3]中的思路已经被纳入到许多商业优化器中,并且仍然具有明显地关联性。在这里,我将基于 Select-Project-Join(SPJ) 查询的上下文,介绍下这些重要思路中的部分。SPJ 查询类与连接查询(conjunctive queries)密切相关,并封装了连接查询,连接查询在数据库理论中得到了广泛的研究。
在 SPJ 查询上下文中,System-R 优化器的搜索空间由算子树组成,算子树对应了线性序列的连接操作,例如:Join(Join(Join(A,B),C),D) 的序列如图 2(a) 所示。由于连接的结合性和交换性,这些序列在逻辑上是等价的。连接算子既可以使用嵌套循环(nested loop)实现,也可以使用排序合并(sort-merge)实现。每个扫描节点即可以使用索引扫描(使用聚集或非聚集索引),也可以使用顺序扫描。最后,谓词应当尽可能早地进行计算。
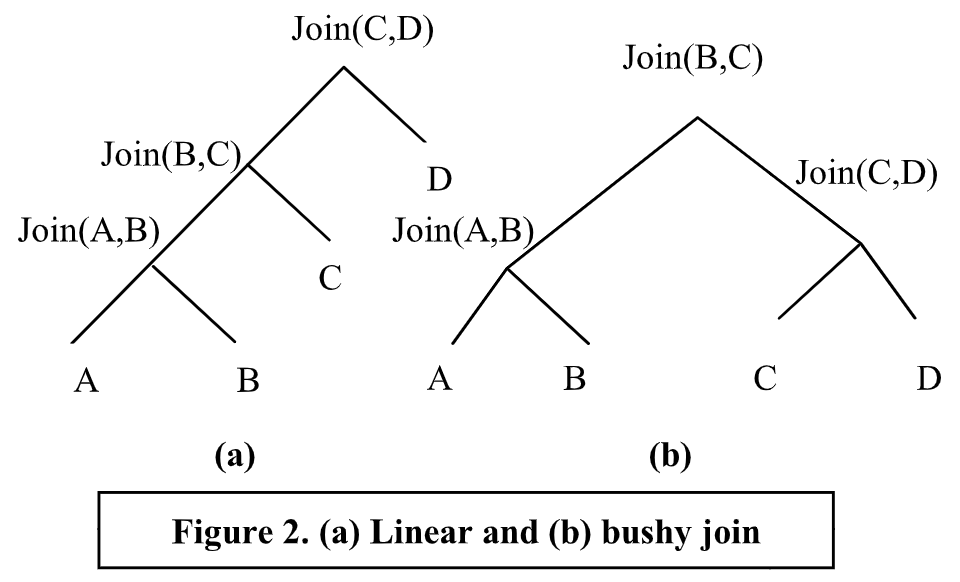
成本模型将估算的成本,分配给搜索空间中的任何部分或全部执行计划。它还决定了执行计划中,每个算子输出的数据流的估算大小。成本模型依赖于:
一组维护在关系和索引上的统计数据,例如:关系中数据页的数量、索引中的页数以及某一列不同值的数量;
用于估算谓词选择性以及预测每个算子节点输出数据流大小的公式。例如:通过取两个关系大小的乘积,然后使用所有适用谓词的连接选择度来估算连接输出的大小;
估算每个算子执行查询的
CPU和I/O开销的公式。这些公式考虑了输入数据流的统计属性、输入数据流的既存访问方法以及数据流上的任何可用的顺序(例如,如果一个数据流是有序的,那么在该数据流上,排序合并sort-merge连接的成本可能会显著降低)。此外,还会检查输出数据流是否有任何顺序。
成本模型使用上述 1~3 中的信息,为执行计划中的算子以自底向上的方式进行计算并关联以下信息:(1)算子节点输出的数据流大小;(2)算子节点输出的数据流创建或维持的元组的顺序;(3)为算子估算执行成本(以及部分执行计划到目前为止的累计成本)。
System-R 优化器的枚举算法演示了两个重要的技术:使用动态规划(dynamic programming)和使用感兴趣的顺序(interesting orders)。
动态规划方法的本质是基于成本模型满足最优原则的假设。具体地说,它假设为了获得由 k 个连接组成的 SPJ 查询 Q 的最优计划,只要考虑由 (k - 1) 个连接组成的查询 Q 的子表达式的最优计划,并用一个额外的连接扩展这些计划即可。换句话说,在确定 Q 的最优方案时,不需要进一步考虑由 (k - 1) 连接组成的查询 Q 的子表达式(也称为子查询)的次优方案。因此,基于动态规划的枚举将 SPJ 查询 Q 看作一组关系 {R1, . .n} 的连接。枚举算法是自底向上的。在第 j 步的最后,算法为所有大小为 j 的子查询生成最优执行计划。为了获得由 (j + 1) 个关系组成的子查询的最优执行计划,我们考虑了为子查询构建执行计划的所有可能方式,通过扩展第 j 步构建的执行计划。
动态规划方法的本质是基于成本模型满足最优原则的假设。具体地说,它假设为了获得由k个连接组成的SPJ查询Q的最优计划,只考虑由(k-1)连接组成的Q子表达式的最优计划,并用一个额外的连接扩展这些计划。换句话说,在确定Q的最优方案时,不需要进一步考虑由(k-1)连接组成的Q的子表达式(也称为子查询)的次优方案。因此,基于动态规划的枚举将SPJ查询Q视为一组关系{R1, . .n}被加入。枚举算法是自底向上的。在j的最后一步,所有子查询的算法生成最优计划规模j。获得一个最优的计划组成的子查询(j + 1)关系,我们考虑所有可能的子查询的方法构造一个计划通过扩展计划建造在j - th一步。例如,{R1, R2, R3, R4}通过从最优方案中选取成本最便宜的方案来获得:(1)Join({R1, R2, R3}, R4(2)加入({R1, R2, R4}, R3(3) Join ({R1, R3, R4}, R2(4)加入({R2, R3, R4}, R1).{R1, R2, R3, R4}可以被丢弃。动态规划方法比naïve方法快得多,因为与O(n!)计划相比,只有O(n2)计划n -1)计划需要列举。System R优化器的第二个重要方面是考虑感兴趣的订单。现在让我们考虑一个表示{R之间连接的查询1, R2, R3}和谓词R1。= R2。= R3。。我们还假设子查询{R1, R2}分别为x和y用于nested-loop和sort-merge join, x < y。此时,考虑{R1, R2, R3},我们将不考虑R1 和R2 使用排序合并连接。但是,请注意,如果使用排序合并来连接R1 和R2,则对连接的结果在a上进行排序,排序后可以显著降低与R连接的代价3.因此,裁剪表示R之间排序合并连接的计划1 和R2 可能导致全局计划的次优性。问题的出现是因为R之间的排序归并联接的结果1 和R2 元组的排序
在后续联接中有用的输出流。但是,嵌套循环连接没有这样的顺序。因此,给定一个查询,System R识别可能对查询的执行计划产生影响的元组的顺序(因此命名为感兴趣的顺序)。此外,在System R优化器中,只有当两个计划表示相同的表达式并且具有相同的感兴趣顺序时,才会比较它们。有趣顺序的概念后来在[22]中被推广到物理性质,并在现代优化器中被广泛使用。直观地说,物理属性是计划的任何特性,该特性不为同一逻辑表达式的所有计划共享,但可能影响后续操作的成本。最后,需要注意的是,System-R考虑物理属性的方法展示了一种简单的机制,可以处理任何违背最优原则的情况,而不仅仅是由于物理属性引起的。
尽管System-R方法很优雅,但是框架不能很容易地扩展到包含其他扩展搜索空间的逻辑转换(除了连接排序)。这导致了更可扩展的优化体系结构的开发。然而,基于成本的优化、动态规划和有趣的订单的使用强烈地影响了优化的后续发展。
搜索空间
统计和成本估算
枚举架构
基础优化之外的话题
参考文档
欢迎关注
欢迎关注「端小强的博客」微信公众号,会不定期分享日常学习和工作经验,欢迎大家关注交流。

Melton, J., Simon A. Understanding The New SQL: A Complete Guide. Morgan Kaufman. ↩︎
Graefe G. Query Evaluation Techniques for Large Databases. In ACM Computing Surveys: Vol 25, No 2., June 1993. ↩︎
Selinger, P.G., Astrahan, M.M., Chamberlin, D.D., Lorie, R.A., Price T.G. Access Path Selection in a Relational Database System. In Readings in Database Systems. Morgan Kaufman. ↩︎
